Revista de Educación Andrés Bello, Nº4, 2016, pp.54-86.
ISSN 0719-7403 versión en línea
Recibido: 1 agosto 2016
Aceptado: 20 octubre 2016

1. ESTUDIO DEL PROBLEMA Y PLANIFICACIÓN DE SOLUCIONES

1.1. Introducción

A partir del año 2012 en la asignatura Álgebra y Geometría Analítica I de la Universidad Nacional de La Matanza se realizaron dos actividades simultáneas: el desarrollo de un Proyecto de Investigación (PROINCE- C126) titulado “Nueva propuesta para la enseñanza del Algebra Lineal en el contexto de las carreras de Ingeniería de la UNLaM” y por otro lado la participación en el PEICB: Plan Estratégico de Ingeniería para las Ciencias Básicas que se llevó a cabo en el DIIT de dicha universidad.

El proyecto y el trabajo desarrollado tuvieron por objeto estudiar el proceso de enseñanza-aprendizaje del Algebra Lineal en los alumnos del DIIT con la finalidad de mejorarlo y adecuarlo a las necesidades de las carreras que se dictan en él.

Una de las motivaciones para realizar esta investigación es la dificultad que cotidianamente presentan los alumnos de álgebra en la apropiación, utilización, aplicación y transferencia inter e interdisciplinar de los conceptos que la conforman; por tal motivo, se pretendió indagar y seleccionar los contenidos necesarios y sus relaciones y diseñar e implementar en el proceso de su enseñanza-aprendizaje métodos de trabajo en el aula y actividades que facilitasen una conceptualización correcta e integral de los contenidos seleccionados.

2. TEMA DE ESTUDIO

La problemática en el aprendizaje del Algebra Lineal es un tema que preocupa a los educadores.

En 1962 un grupo de matemáticos notables (Ahlfors, Bellman, Courant, Coxeter, Kac, Lax, Morse, Polya, Weil, entre otros) suscribieron un documento en el cual advertían el error de confeccionar un currículum escolar que privilegiara la abstracción en desmedro de las conexiones de la matemática con las otras ciencias. El documento en cuestión fue publicado en The Mathematics Teacher y en el American Mathematical Monthly.

En el mismo sentido, en el año 1990 se constituyó el Linear Algebra Curriculum Study Group (LACSG[1]), conformado por David Carlson, Charles R. Johnson, David C. Lay y A. Duane Porter con el objetivo de mejorar el currículo de Algebra Lineal. Para este grupo de investigadores también es importante apartarse de la abstracción generada desde el formalismo en vías de un acercamiento a lo concreto, teniendo en cuenta la relación del álgebra con otras áreas del conocimiento. Por tal motivo recomiendan otorgarle una orientación matricial e incorporar la tecnología ya sea en las aplicaciones como en el proceso de enseñanza–aprendizaje en sí mismo.

Actualmente varios grupos de investigadores se encuentran trabajando sobre la didáctica del Algebra Lineal. En Francia existe un grupo integrado por Jean Luc Dorier, Aline Robert, Jacqueline Robinet, Marc Rogalski y Michele Artigue entre otros; en Canadá Anna Sierpinska y Joel Hillel y en EE.UU Guershon Harel y Ed Dubisnky.

Por otro lado, varios estudios de diagnóstico dirigidos por Dorier, Robert, Robinet y Rogalski[2] entre 1987 y 1994 dan cuenta de un solo obstáculo macizo que aparece en todas las generaciones de estudiantes y para casi todos los modos de enseñar, lo que los autores llamaron el obstáculo del formalismo. De igual modo, investigaciones realizadas por Dorier y Sierpinska en torno al aprendizaje del Algebra Lineal reportan que las dificultades se originan por los diversos lenguajes que se utilizan –geométrico, aritmético, algebraico– y muchas veces sin articulación.

Es desde esta perspectiva que se planteó la investigación cuya propuesta consistió en reformular los contenidos programáticos de la materia álgebra lineal tanto en su aspecto conceptual como metodológico, desde una visión integradora y relacional, respetando los contenidos mínimos fijados por las Resoluciones de acreditación de las diferentes carreras de Ingeniería y en crear un ámbito de discusión en vías de perfeccionamiento del saber y de la práctica docente en ésta área del conocimiento.

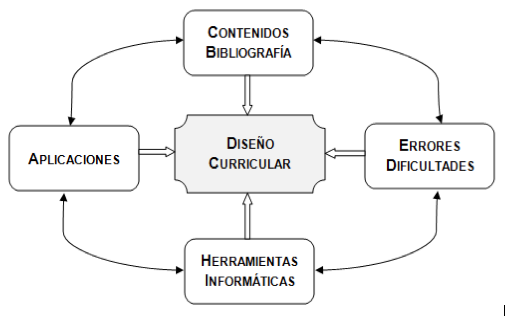
El trabajo se realizó a partir de una metodología tanto cualitativa como cuantitativa, utilizando datos primarios y secundarios extraídos de diversas fuentes y trabajando las dimensiones teóricas y prácticas de los distintos contenidos del álgebra a partir de los siguientes ejes interrelacionados:

Contenidos y Bibliografía, este eje contempló varios aspectos: a) el buceo bibliográfico de contenidos del Álgebra Lineal desde la perspectiva de su génesis histórica y epistemológica que incumban a la necesidad de formación de los ingenieros, b) las relaciones conceptuales entre los contenidos, c) el análisis de investigaciones realizadas sobre la enseñanza del Álgebra y d) la opinión de los docentes de las distintas áreas de conocimiento que conforman la currícula de las carreras de Ingeniería.

Errores y dificultades, en este caso el estudio realizado consistió en la detección y sistematización de los errores comunes y dificultades presentadas por los alumnos en distintos temas de álgebra. El mismo se llevó a cabo a partir del análisis de evaluaciones previas de grupos de alumnos de 6 cursos y 3 cuatrimestres diferentes.

Aplicaciones, este eje tuvo por finalidad la búsqueda y elaboración de problemas de aplicación para los distintos contenidos tratados con la finalidad de acercar al alumno a actividades específicas de la Ingeniería, que sean accesibles al nivel del desarrollo que éste posea y que permitan intentar, en la medida de lo posible, actividades de aprendizaje basadas en la resolución de problemas reales vinculados con la formación profesional.

Herramientas informáticas, consistió en el análisis de software –de uso libre o no – que pueda utilizarse en el desarrollo de la materia con la incorporación de actividades conexas, con el interés particular de que los alumnos puedan participar activamente en la resolución de problemas utilizando esos programas y que incorporen en forma natural la modalidad de trabajo con dichos auxiliares informáticos, de manera similar a lo que tendrán que hacer durante su futura vida profesional.

Estos ejes de estudio, confluyeron en la elaboración de un diseño curricular en el que la interrelación entre ellos tiende a favorecer el carácter dinámico de la ciencia:

Para probar el diseño elaborado, se tuvieron en cuenta tres etapas: previa, durante y posterior a la implementación.

En la etapa previa a la implementación:

-Se elaboraron y seleccionaron las estrategias referidas al proceso de enseñanza aprendizaje: las de motivación, las de elaboración, las de organización, las de recuperación y de evaluación.

-Se confeccionó el material teórico – práctico a utilizar en el aula y,

-Se seleccionó y preparó a los docentes que formarían parte del proceso.

La etapa de implementación se llevó a cabo en dos cursos pilotos: uno del turno mañana y otro del turno noche. En la misma:

Se trabajó con el material elaborado en la modalidad de aula taller.

-Se evaluó al alumno en forma permanente, antes, durante y al finalizar el proceso.

-Al terminar el curso se tomó una encuesta de opinión a los alumnos que intervinieron en la experiencia.

Finalmente, en la etapa posterior, se llevó a cabo el análisis de los resultados obtenidos por los alumnos, de la encuesta de opinión y de la actividad realizada por los docentes.

3. DESARROLLO DE LA INVESTIGACIÓN^[3]

3.1. Contenidos y buceo bibliográfico

Se trabajó en el análisis del abordaje curricular y pedagógico efectuado por diferentes autores de textos accesibles a los alumnos para un curso de Algebra Lineal (AL). Algunas de las ideas más destacadas extraídas hasta el momento se expresan a continuación

En 1990 se forma el The Linear Algebra Curriculum Study (LACSG) con el fin de producir un currículo de Álgebra Lineal – AL – que culmina con las siguientes 5 recomendaciones:

a) Los contenidos y su presentación deben responder a la necesidad de las disciplinas clientes (Física, Ingeniería, Economía, etc.). La generalización y profundización debe realizarse en la medida que el tiempo lo permita.

b) Un primer curso de AL deberá estar fuertemente orientado a matrices. Se sugiere menos abstracción, más énfasis en la resolución de problemas y aplicaciones motivadoras, yendo desde lo concreto hacia lo más conceptual.

c) Considerar las necesidades e intereses de los estudiantes como aprendices. Buscar una metodología de enseñanza-aprendizaje activa, sin olvidarse de los saberes previos de los alumnos.

d) Usar tecnología.

e) Un segundo curso de AL con un sesgo más conceptual y de mayor justificación teórica[4].

Harel (1997), Dubinsky (1997), Day y Kalman (1999), Uhlig (2002; 2010) y Dorier (2002) son algunos de los autores analizados en el proyecto. Se trabajó además sobre un método de instrucción desarrollado por Eric Mazur en Física, basado en el método de Instrucción de Peer, el cual a pesar de estar en un aula amplia y con muchos alumnos utiliza un eficaz método colaborativo.

En el análisis de los libros de textos adecuados a las nuevas pautas de enseñanza del Álgebra Lineal se pueden citar a: Poole (2004), Nakos (1999), Grossman (1988), Lay (2012).

3.2. Encuesta a Jefes de Cátedra

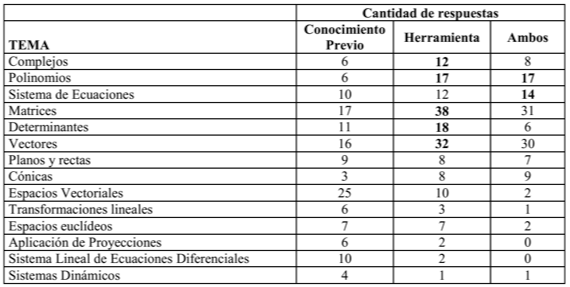
Como complemento del buceo bibliográfico y con la finalidad de indagar en los contenidos de Álgebra Lineal que se necesitan y utilizan en las materias posteriores al Ciclo Básico Común de las carreras del DIIT, se confeccionó una encuesta dirigida a los Jefes de Cátedra. En la encuesta, se consultó sobre el tipo de contenido y la utilización que hacen de ellos: como conocimientos previos para avanzar o profundizar en otros temas, como herramienta matemática, ambos usos u otros no especificados[5].

De las respuestas obtenidas surge que los temas más requeridos por los profesores son: los métodos de resolución de un sistema de ecuaciones en un 72,4%, la caracterización de las soluciones de un sistema de ecuaciones con el 51,7%, las operaciones entre matrices con el 62% y las operaciones entre vectores en un 51,7% (apéndice, tablas 1 y 2)

Por otro lado, en relación a la utilización, en casi todos los casos predomina el uso de los mismos como herramienta.

3.3. Herramientas Informáticas

Analizar los recursos informáticos del tipo CAS (sistemas algebraicos de computación) ha llevado a confeccionar un breve informe sobre los que se encuentran disponibles.

Como el abanico de elección es muy amplio, el análisis fue reducido a un subconjunto pequeño en cuanto a posibilidades de evaluación, experiencia de trabajo sobre los mismos, pros y contras pensadas en función de las limitaciones del lenguaje de programación que pueden conocer los alumnos, accesibilidad a los recursos, etc. Ellos son: Mathematica, MatLab, SAGE, Maxima, Derive, SCILAB. Se recomendó el uso del MatLab o de algún sucedáneo.

3.4. Análisis de errores

Los errores son parte indispensable del proceso de aprendizaje. Identificar los cometidos por sus alumnos le permite al docente replantear estrategias de enseñanza e intervenir de una manera más eficaz sobre las dificultades observadas.

Entre diversas categorizaciones o clasificaciones de errores, se tomaron como referencia a la dada por Radatz (1979, 1980) y recuperada por Rico (1995), así como también la debida a Mosvshovitz-Hadar, N.; Inbar, S.; Zaslavsky, O. (1987).

En este trabajo se propone una nueva clasificación de errores que, si bien está relacionada con las anteriores, consideramos se adecua mejor a los errores observados y permite un análisis transversal sobre los contenidos evaluados.

Además, se propuso tipificar los errores más comunes en algunos contenidos de Álgebra Lineal tomando en cuenta dos grandes grupos: errores en los conceptos teóricos involucrados y errores debido a los procedimientos utilizados por los alumnos.

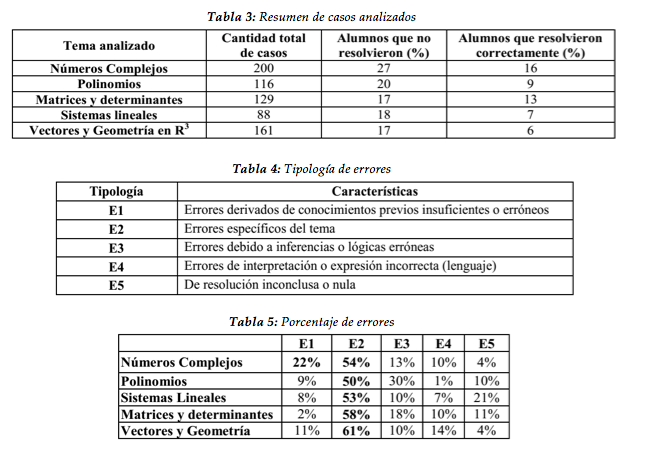
Se procedió a elaborar dimensiones a modo de ítems de análisis en los que se observaron los exámenes de la asignatura sobre los temas Polinomios, Números Complejos, Matrices y determinantes, Sistemas lineales y Vectores y Geometría en R³. Estos ítems se utilizaron para distintos grupos de alumnos.

En el apéndice, las Tablas 3, 4 y 5 muestran un resumen de los resultados obtenidos.

3.5. Aplicaciones

A partir de un minucioso análisis de texto (ver bibliografía específica) se han seleccionado varios tópicos como ser circuitos eléctricos, balanceo de ecuaciones químicas, flujo poblacional (utilización de cadenas de Markov), tránsito en la ciudad, modelos de interacción en Sociología, trabajo de una fuerza, aproximación polinomial de una serie de puntos, coordenadas homogéneas y su uso en computación gráfica, transmisión del calor y temperaturas medias en una placa metálica, función de Demanda en Economía y Modelo de Leontief[6].

3.6. Pre Diseño Curricular

Este diseño, resultado de los estudios desarrollados en la presente investigación, se presentó, a instancias del DIIT, al Grupo de Trabajo del “Diseño de un proyecto formativo para el ciclo de ciencias básicas en el marco de las metodologías activas de enseñanza” (PEICB 2013); con el fin de actualizar las metodologías y los recorridos didácticos en las materias de Ciencias Básicas del Ciclo Básico Común.

A partir del pre diseño curricular elaborado, se realizó la implementación en el aula durante el segundo cuatrimestre del 2013. La misma se llevó a cabo en dos comisiones de Álgebra Lineal, una del turno mañana y otra del turno noche con respectivamente 81 alumnos inscriptos y 4 docentes y 59 alumnos y 3 docentes. Para garantizar la implementación de la nueva metodología de trabajo se eligió como docentes responsables de cada una de las comisiones a integrantes del grupo de investigación[7].

El diseño sobre el que se trabajó fue denominado Tejiendo el Algebra Lineal en consonancia con la idea de una construcción continua, trabajosa y en forma de red de los contenidos a abordar en un curso inicial de Algebra Lineal y Geometría Analítica.

En esta primera versión tuvieron un lugar preponderante las ideas extraídas y adaptadas de los autores anteriormente citados en página 4 y otros[8]. En el apéndice se puede acceder a una versión sintética del mismo.

4. IMPLEMENTACIÓN DE LA REFORMA

4.1. La modalidad de trabajo en el aula

Muchas preguntas guiaron la búsqueda de una nueva metodología de trabajo.

Uhlig (2010) nos interroga sobre varias cuestiones:

-¿Por qué aún enseñamos Matemática hoy en día?, ¿Por qué enseñar Algebra Lineal y teoría de Matrices?

-¿En dónde está la dificultad para aprender (por ejemplo) dependencia e independencia lineal?

Se precisan saber las ideas previas de los alumnos y conocer sus motivaciones: “No puedo enseñar en el vacío: construyo sobre lo que otros docentes ya han realizado. Como docente debo desafiarme a mí mismo continuamente para comprender mejor.

Ser exitoso en la enseñanza es poder transmitir los principios elementales de la disciplina a las generaciones siguientes y ayudar a los alumnos no solo a memorizar sino a responder antes preguntas y problemas no estándares. Pero, ¿estamos limitados al conocimiento que nos fue dado hace décadas cuando éramos estudiantes?

Así repetimos como una tradición lo que nos dieron nuestros profesores que a su vez lo tomaron de otros. ¿Por qué esto? ¿Por qué no cambiar según nuestra propia experiencia y conocimiento disciplinar? ¿Es qué no sabemos más?

A menos que el círculo se rompa por nosotros y nos convirtamos en responsables personales para los contenidos de nuestro curso y su presentación, no hay y no habrá cura para aprender en un curso de Algebra Lineal.

“Si queremos que las matemáticas vivan, cada uno de nosotros debe enseñar de una manera viva.”

Los alumnos recién comienzan a transitar su historia universitaria. Pocos conocimientos claros, ideas previas erróneas, falta de dedicación y motivación al estudio. Es un hecho que la gran mayoría no leyó un libro de texto matemático en su vida, pero ¿es la exposición de un docente en el pizarrón el medio idóneo para cambiar la inercia que tienen?

Lo central de la propuesta es virar a un aprendizaje participativo en consonancia con una inversión pedagógica. El alumno aprende activamente durante todo el desarrollo de cada clase del tipo aula-taller y el docente tiene la misión de andamiar dicho proceso a través de explicaciones puntuales, sugerencias, cuestionamientos o reafirmación de los pasos elegidos. Conseguir un aprendizaje activo no tiene una única receta. Pensamos que se puede realizar desde diferentes abordajes metodológicos sin necesidad de ser éstos excluyentes entre sí; el aprendizaje será una actividad colectiva pero su internalización es netamente individual y es ella la que sabe cuánto tiempo le demanda alcanzarlo.

Nuestra propuesta tiene como foco los siguientes elementos:

-Un aprendizaje autorregulado apoyado por un apunte práctico-teórico, claro, no elemental pero acotado en las justificaciones teóricas –léase demostraciones-, que vaya introduciendo al alumno lo más naturalmente posible en el tema a abordar y que lo obligue a trabajar en simultáneo. Aprender conceptos a través de ejemplos para luego alcanzar la generalización que sea más pertinente.

-Un andamiaje permanente sobre la actividad del alumno, clarificando contenidos, suministrar ejemplos adicionales, producir cuestiones que permitan el conflicto cognitivo.

-Un control recurrente sobre los avances y retrocesos que tuviere cada alumno, sobre la actitud y dedicación del alumno para con su aprendizaje. Utilizar la evaluación no como elemento punitivo sino pensarla como otro momento del proceso de enseñanza-aprendizaje. Así que la propuesta incluye evaluaciones formativa y sumativa, informal y formal.

-Realimentación inmediata sobre el alumno para indicarles los avances obtenidos y las dificultades que aún permanecen. Esta actividad debe estar acompañada por una fuerte motivación en pos de conseguir de cada alumno lo mejor que puede dar y evitar la angustia que pudiera formarse.

-Favorecer conductas apropiadas para el aprender a aprender. Del control externo se debiera poder llegar a la autoexigencia interior. El alumno tiene que darse cuenta de que aprende para sí y no por los controles externos que hubiere.

-Vincular fuertemente los contenidos teóricos con las aplicaciones que a un ingeniero pudieran presentársele, reconociendo el carácter instrumental de las Matemáticas. Las aplicaciones serán un elemento nodal para el desarrollo de un aprendizaje basado en problemas.

A continuación, el devenir de una clase tipo.

a) Se toma un mini test individual o grupal según lo amerite. Se trata de un ejercicio, problema o cuestión teórica reducida –y que les lleve poco tiempo–. Mientras abordan la fase b), los docentes corrigen lo realizado y se vuelca en una planilla el desempeño del alumno.

b) Los alumnos rearman los grupos de no más de 4 integrantes. Comienzan la lectura del apunte y la resolución de actividades sugeridas. La clase es repartida entre los docentes haciéndose cargo del andamiaje de una parte de la misma. Aclaraciones, suministro de otros ejemplos, preguntas adicionales, apoyatura teórica son algunas de las actividades a desarrollar. Estas pueden ser grupales o individuales

c) Cada tanto (1 hora o según se crea necesario) procedemos utilizando el método de instrucción de Peer. Se da a toda la clase una pregunta-ejercicio que por grupos resuelven y entregan las respuestas al docente-coordinador de dicha actividad –situación de votación o voting-. Se presentan las respuestas a toda la clase; se estudian y contrastan las diferencias y similitudes. Si lo estudiado durante la clase parece no haberse entendido se explica o se suministran ejemplos adicionales según sea necesario.

d) Cada grupo deberá ir llenando una minuta de lo realizado durante la clase que generalmente incluirá una actividad de complejidad variable a entregar antes de retirarse de la clase. La misma será corregida para la clase siguiente, volcada una nota en la planilla de seguimiento del alumnado y será devuelta al grupo en la clase siguiente. Evaluación permanente.

Notar que diariamente el alumno es evaluado por lo menos 2 veces de manera formal y varias veces de manera informal (en el trabajo sobre cada grupo de cada docente). La intención es ir recreando una historia formativa del alumno en la materia y converger a lo largo del trimestre en la asignación de una nota de “laboratorio” que tenga un peso de 1/3 en la nota final de la materia.

e) Antes de finalizar la clase –que no tiene que ser simultánea en todos los grupos- se señala que contenidos se suponen abordados durante la jornada de aprendizaje para que cada grupo/individuo pueda completar lo faltante en casa o pedir las aclaraciones que precise para la siguiente clase.

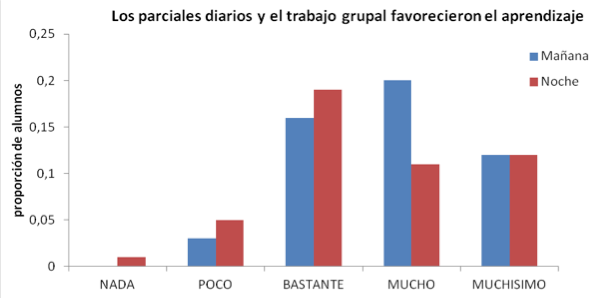
Durante el curso piloto, la evaluación del aprendizaje se realizó durante todo el proceso por medio de parcialitos periódicos (a carpeta abierta) en casi todas las clases (en total se tomaron 20), de trabajos grupales (inicialmente en clase y luego como tarea para la clase siguiente, en total 18) y de una calificación que asignó el docente al desempeño de cada grupo. Todas las instancias de evaluación conformaron una nota de laboratorio que se promedió (en forma ponderada) con la nota obtenida en cada uno de los dos parciales formales. De esta manera se logró implementar una evaluación permanente.

Se buscó generar en el aula un ambiente de aprendizaje-enseñanza (no es antojadiza la inversión en la palabra compuesta como no lo es en clase práctico-teórica) dinámico, alegre, con un efervescente trabajo intergrupal, con docentes y alumnos que interactuaran de una manera viva.

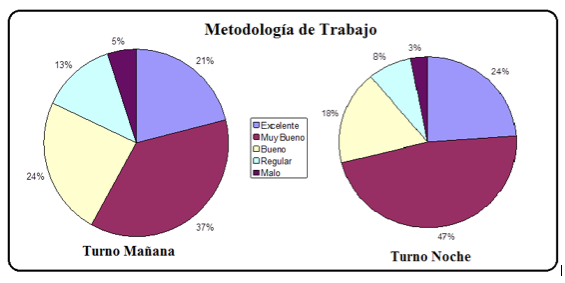
Para evaluar la modalidad de trabajo en el aula, al finalizar el período de clases se encuestó a los alumnos sobre su opinión respecto a: la metodología utilizada, el material de trabajo, la evaluación, el ambiente generado y la labor docente[9].

4.2. El recorrido conceptual

El diseño de los contenidos se pensó espiralado en la complejidad y cercano a la idea que las guías de trabajo sucesivas tratan de ampliar, contener, generalizar y en algunos casos reformular lo ya visto; simultáneo en el abordaje de los ejes conceptuales del Algebra Lineal ya que desde el comienzo se trabajaron cuestiones geométricas como los movimientos en el plano, sistemas de ecuaciones, nociones de transformación lineal, vectores y espacios vectoriales.

Para el recorrido conceptual, plasmado en el material elaborado y en el trabajo en el aula se tuvieron en cuenta los siguientes aspectos:

a) El mismo se inició desde las cuestiones geométricas en el plano como lo son las traslaciones, simetrías centrales y axiales, las rotaciones y las proyecciones ya que:

-en el curso de ingreso se ha abordado a través de construcciones con lo cual se facilita la indagación de ideas previas y sirve como base para nuestra construcción teórica –subsumidor ausubeliano-;

-ayuda en la visualización y ejemplificación de otros conceptos (como ser transformaciones lineales);

-a pesar de que en la escuela media la Geometría está un tanto relegada, facilita el acercamiento del alumno hacia lo abstracto desde algo más concreto (cercano sería una palabra más acorde);

-sirve como soporte para la presentación de nuevos entes matemáticos y sus operaciones –por ejemplo, vectores.

b) El segundo mojón fue vincular las transformaciones geométricas con sistemas de ecuaciones lineales y con trasformaciones lineales; a los vectores sus propiedades y sus operaciones –distintas a las de los números reales- como casos especiales de otras estructuras más generales (los espacios vectoriales).

c) A partir de vectores se desarrolló el estudio de rectas (en el plano y en el espacio) y el plano (incluyendo intersección, inclusión, paralelismo, perpendicularidad, distancia). Se muestra la pertinencia de trabajar más sistemáticamente al resolver sistemas de ecuaciones lineales (lo que hace preciso introducir matrices con sus operaciones y conformando nuevos espacios vectoriales) y se enfatiza el hecho que éstas tienen: una mirada geométrica en el espacio (como planos), otra como combinación lineal de vectores, una tercera matricial y una cuarta como transformación lineal (se puede pensar si el vector de términos independientes está o no en la imagen de la transformación, o como ceros de ésta para sistema de homogéneos).

d) La vinculación de los conceptos del Algebra y otras disciplinas: Criptografía, Economía (ingreso, costo; modelo de Leontief), Sociología, Cadenas de Markov (flujo poblacional, preferencias, etc.), Física (descomposición de fuerzas, trabajo, electricidad, transmisión de calor), Química (equilibrio de ecuaciones), Matemática (interpolación por polinomios), Meteorología, Tránsito en la ciudad y Genética.

5. RESULTADOS DE LAS ENCUESTAS[10]

 

La encuesta fue respondida por 38 alumnos del turno mañana y 38 del turno noche:

Durante el segundo cuatrimestre de 2013, la materia Álgebra Lineal se dictó en 8 comisiones: 3 del turno mañana, 1 del turno tarde y 4 del turno noche, para un total de 489 alumnos.

Para implementación de la nueva metodología de trabajo se seleccionó un curso del turno mañana y uno del turno noche, por ser los turnos más representativos.

La asignación de los alumnos a dichas comisiones fue aleatoria, es decir que en el momento de la inscripción no se informó qué cursos participarían de la experiencia.

La distribución del total de inscriptos resultó de 140 alumnos para el nuevo diseño (81 a la mañana y 59 a la noche) y 349 para el tradicional (155 a la mañana, 47 a la tarde y 147 a la noche).

Los resultados finales de la cursada, diferenciando por el tipo de metodología aplicada se presentan en la siguiente tabla en la que se diferenciaron los tipos de ausente en alumnos que no participaron de ninguna evaluación y aquellos alumnos que participaron del curso hasta la primera evaluación parcial[11].

Se observa que en los cursos donde se aplicó la nueva metodología es un poco mayor la retención de los alumnos.

La aseveración anterior puede corroborarse estadísticamente utilizando la prueba Chi-cuadrado, es decir que la condición final de los alumnos depende significativamente del tipo de metodología empleada en los cursos (p = 0,02)

La afirmación anterior no se confirma si se consideran sólo los alumnos que siguieron la materia (condición sin los ausentes).

6. CUESTIONES A REVISAR ACERCA DE LO METODOLÓGICO

a) El abordaje tan espiralado resultó útil desde lo pedagógico pero incompatible con los tiempos para incluir todos los temas que precisa un curso de Algebra Lineal.

b) Se podrían unificar contenidos como ser rectas en el plano y en el espacio y sistemas de ecuaciones de 2 con 3 o más incógnitas.

c) Los cursos de la noche disponen de menos tiempo por clase pues los alumnos llegan tarde del trabajo y suelen retirarse un rato antes de la finalización por cuestiones de transporte y seguridad. Se piensa en la complementación a través de una plataforma virtual y clases de consulta[12].

d) Un cronograma preciso sobre actividades a realizar en el aula, a completar y/o producir fuera de ella. El mismo permite que cada alumno, docente, curso y materia en general avancen aproximadamente sincrónicamente.

e) Capacitar a todo el Staff docente con la metodología de trabajo en aula y fuera de ella. Por lo experimentado se precisa un importante involucramiento de parte de cada profesor.

f) Producir guías adicionales con más ejercitaciones y de diversa índole, consignas teóricas, explicaciones y desafíos adicionales y un poco de material no obligatorio pero ampliatorio de ciertos contenidos (como podrían ser las aplicaciones).

g) Por cuestiones de tiempo sólo se pudo realizar una guía docente comentada de la unidad I donde se comentaban las ideas–fuerza que sustentaban el recorrido curricular que se estaba desarrollando y cuestiones metodológicas.

h) Mantener la evaluación continua con un parcialito por clase, pero espaciar semanalmente el trabajo grupal (tal vez más largo y cada dos clases).

i) La falta de tiempo impidió utilizar el método de Instrucción de Peer con cuestiones pequeñas a lo largo de cada clase. Creemos que sería de suma utilidad, pero habrá que encontrarle la manera más conveniente de poder llevarlo a cabo.

j) No se contó con un aula interactiva donde poder trabajar con algún software de los investigados.

7. LA REFORMA SUSTENTADA EN EL TIEMPO

En el primer cuatrimestre del 2014 la reforma fue implementada en todos los cursos. En ese período los docentes tuvieron que adaptarse a la nueva metodología y a los nuevos contenidos.

Durante el devenir de los cuatro cuatrimestres de los años 2014 y 2015 se fueron espaciando los parcialitos y los trabajos grupales. Surgió que algunos alumnos no concurrían el día que no había parcialito o entrega de trabajo grupal. No todos reemplazan la ausencia con el estudio en casa.

Para el período lectivo 2016 se avizoran restricciones presupuestarias y la cantidad de docentes por curso serán dos. Por eso debemos prescindir del trabajo grupal con nota pues la corrección de los mismos conlleva una carga laboral más allá de lo que la carga docente amerita. Los mismos se agregaron a los apuntes práctico-teóricos.

Para poder reducir las ausencias se implementarán en cada clase evaluaciones formativas que podrán ser parcialitos (de 45’ de duración, a desarrollar) o tests (de 20’, de respuesta corta, sin entrega de desarrollos); teniendo éstos últimos menor peso en la nota de laboratorio.

Esto permitirá además evaluar sobre bases objetivas el esfuerzo y participación personal de cada alumno.

REFERENCIAS

 

Bibliografía general

Berriochoa, Elías; Cachafeiro, Alicia; Illán, Jesús (2009): “An Approach for teaching the Linear Algebra for students of Engineering”, Proceedings of ICERI 2009 Conference, Madrid.

Carlson, David; Johnson, Charles; Lay, David; Cuane Porter, A.; Watkins, Ann; Watkins, William (editores), (1997):” Resources for teaching Linear Algebra”, Mathematica Association of America – MAA Notes, Vol. 42.

Carlson, David; Johnson, Charles; Lay, David; Porter, A. Duane, (Jan., 1993): “The Linear Algebra Curriculum Study Group Recommendations for the First Course in Linear Algebra”. The College Mathematics Journal, Vol. 24, No. 1, pp. 41-46.

Dikovic, Ljubica (2007): “Interactive Learning and Teaching of Linear Algebra by WEB Techonologies: Some Examples”, The Teaching of Mathematics 2007, Vol. X, 2, pp. 109–116.

Dorier, Jean Luc (editor), (2002): “On The Teaching of Linear Algebra”, Mathematics Education Library – Vol. 23, Kluwer.

Harel, Gershon (1999): “Student´s understanding of proofs: a historical analysis and implications for the teaching of geometry and linear algebra” en Linear Algebra and its applications, 302-303, 601-613, Elsevier.

Harel, Guershon; Sowder, Larry (1998): “Students´s proofs schemes: results from exploratory Studies”; CBMS Issues in Mathematics Education – Vol. 7.

Sierpinska, Anna; Nnadozie, Alfred & Asuman, Okta (2002): A study of relationships between theoretical thinkings and high achievement in linear algebra. Concordia University.

Contenidos y Bibliografía

Anton, Howard (2000): Introducción al Algebra Lineal. Editorial Limusa, Grupo Noriega Editores, segunda edición, México.

Day, Jane; Kalman, Dan (January, 19, 1999): “Teaching Linear Algebra: What are the Questions?

“http://cimm.ucr.ac.cr/ojs/index.php/eudoxus/article/view/60/42 (17/12/12)

Dorier, Jean Luc (editor): «On the teaching of Linear Algebra”, Mathematics Education Library, Volume 23, Kluwer Academic Publishers, 2002.

Dubinsky, Ed (1997): “Some thoughts on a first course in Linear Algebra at the College Level” en Resources for Teaching Linear Algebra, David Carlson, Charles R. Johnson, David C. Lay, A. Duane Porter, Ann Watkins & William Watkins (editores), The Mathematical Association of America, 1997 (EE.UU.).

Grossman, Stanley (1988): Aplicaciones de Algebra Lineal. Grupo Editorial Iberoamérica, México.

Harel, Herson (1997): “The Linear Algebra Currículo Study Group Recommendations: Moving beyond concept definition” en Resources for Teaching Linear Algebra, David Carlson, Charles R. Johnson, David C. Lay, A. Duane Porter, AnnWatkins & William Watkins (editores), The Mathematical Association of America, 1997 (EE.UU.).

Nakos, George; Joyner, David (1988): Algebra Lineal con Aplicaciones. International Thomson Editores, México.

Poole, David (2004): Algebra lineal. Una introducción moderna. International Thomson Editores, México.

Uhlig, Frank (2002): «A New unified, balanced, and conceptual approach to Teaching Linear Algebra”, en http://cimm.ucr.ac.cr/ojs/ index.php /eudoxus/article/view/57/54 (17/12/12).

Uhlig, Frank (2010): «Questions about Teaching, Teaching Mathematics and Teaching Linear Algebra” en http://matrix.skku.ac.kr/ilas/2010-ILAS-Edu/FUhlig-ILAS-2010.pdf (17/12/12).

Análisis de errores

Caronia, S.; Zoppi,A. N.; Polasek,M.; Rivero, M.; Schwieters, H. (2006). Los conocimientos matemáticos en el umbral de la universidad. Premisa – Año 8 – Nº 30, 13-23.

Rico, L. (1995): “Errores y dificultades en el aprendizaje de las Matemáticas”, cap. 3. pp. 69-108, en Kilpatrik, J.; Gómez, P., y Rico, L.: Educación Matemática. Grupo Editorial Iberoamérica, Méjico.

Socas, M. (2007). “Dificultades y errores en el aprendizaje de las matemáticas. Análisis desde el enfoque lógico semiótico”. Investigación de Educación Matemática XI. Pp. 19-52.

Vera, L.; Volta L. Análisis de errores en evaluaciones de suficiencia ingreso a la Universidad Nacional de Quilmes eje lógico matemático departamento de Ciencia y Tecnología. II Jornadas de Enseñanza e Investigación Educativa en el campo de las Ciencias Exactas y Naturales.

Aplicaciones

Edwards C. H.; Penney, David (1996): Cálculo con Geometría Analítica. cuarta edición, Prentice Hall Hispanoamericana, México.

González, Rafael; Woods, Richard (1996): Tratamiento digital de Imágenes. Addison-Wesley. España.

Kolman, Bernard (2002): Algebra Lineal con Aplicaciones y Matlab. 6ª Edición. Editorial Prentice Hall.

Kraus, John; Fleisch, Daniel (2000): Electromagnetismo con aplicaciones. Editorial McGraw Hill, México.

Lay, David (1999): Algebra Lineal y sus Aplicaciones. Segunda edición, Addison Wesley-Longman, México.

Lindner, Douglas K (1999): Introduction to Signals and Systems. Editorial McGraw Hill Higher Education, EE.UU.

Sears, Francis; Zemansky, Mark; Young, Hugh (2005): Física Universitaria. Undécima edición. Editorial Pearson, México.

Thomas, George; Finney, Ross (1987): Cálculo con Geometría Analítica. Vol. II”. Addison-Wesley Iberoamericana, México.

Herramientas informáticas

Dikovic, Ljubica (2007): “Interactive learning and teaching of linear algebra by web technologies: some examples”. The teaching of mathematics, 2007, Vol. X, 2, pp. 109–116.

Hill, David (2009): Teaching Introductory Linear Algebra Incorporating MATLAB. Temple University, [email protected].

Hogben, Leslie (2007): “Teaching Linear Algebra: Technology and Resources”, Iowa State University, USA, 3rd University Mathematics Courses Forum, Chengdu, China.

Huibin, Wu (2004): “Computer aided teaching in Linear Algebra”, The China Papers, July 2004, School of Science, Beijing Institute of Technology, Beijing.

Xiaoxu, Han (2009): “Teaching Elementary Linear Algebra Using Matlab: An Initial Investigation”, The Scholarship of Teaching and Learning at EMU, Volume 2 Making Learning Visible Article 9, http://commons.emich.edu /sotl /vol2/iss1/9

Pre Diseño Curricular

Kolman, Bernard; Hill, Davis (2006): Algebra Lineal. Pearson Educación, México, octava edición.

Lay, David (1999): Algebra Lineal y sus Aplicaciones. Segunda edición, Addison Wesley-Longman, México.

Lay, David; Mc Donald, Judith (2012): Study Guide of Linear Algebra and Its Applications. Pearson Addison-Wesley, fourth edition.

Meyer, Carl (2000): “Matrix Analysis and Applied Linear Algebra”, SIAM -Society for Industrial and Applied Mathematics.

Nakos, George; Joyner, David (1999): Algebra Lineal con Aplicaciones. International Thomson Editores, México.

Shores, Thomas (2007): Applied linear Algebra and Matrix Analysis. Springer Science+Business Media, USA.

Strang, Gilbert (2007): Algebra Lineal y sus aplicaciones. International Thomson Editores, cuarta edición, México.

Uhlig, Frank (2002): Transform Linear Algebra. Prentice Hall, EE.UU.

Williams, Gareth (2002): Algebra Lineal con aplicaciones. Mc Graw-Hill, Interamericana Editores, Cuarta edición, México.

APÉNDICES

Encuesta a jefes de cátedra

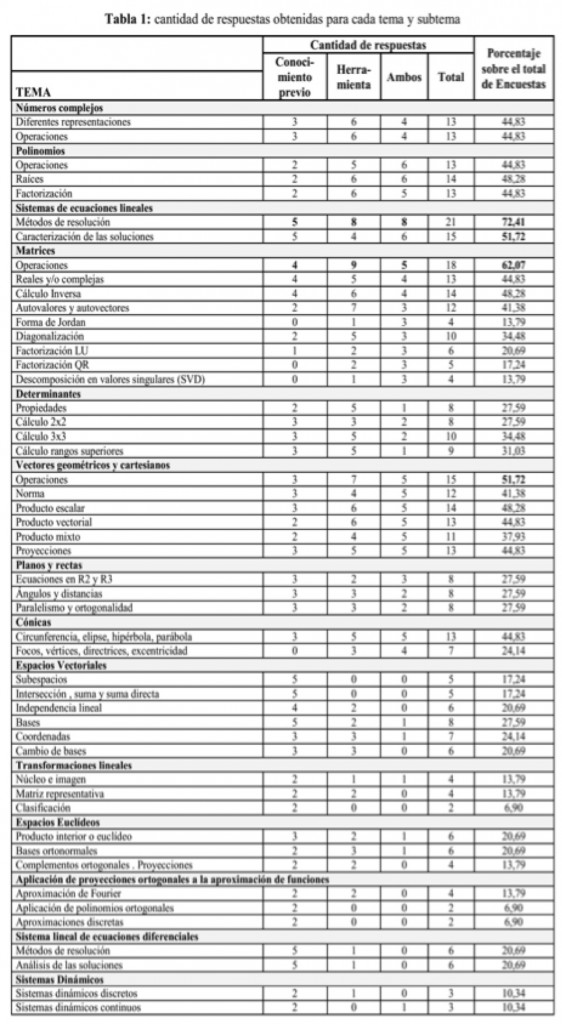
Tabla 2: cantidad de respuestas obtenidas por tema

Analisis de errores

Pre diseño curricular – Tejiendo el Álgebra Lineal

Programa del Recorrido Didáctico de la materia Algebra y Geometría I

NOTAS

[1] The Linear Algebra Currículo Study Group Recommendations: Moving beyond concept definition. Guershon Harel en Resources for Teaching Linear Algebra, David Carlson, Charles R. Johnson, David C. Lay, A. Duane Porter, AnnWatkins & William Watkins (editores), The Mathematical Association of America, 1997 (EE.UU.).

[2] “On the teaching of Linear Algebra”, Mathematics Education Library, Volume 23. Jean Luc Dorier (editor), Kluwer Academic Publishers, 2002.

[3] Lo que sigue es una síntesis del documento final (76 páginas), del proyecto de investigación presentado ante las autoridades departamentales y los evaluadores externos y de la implementación a lo largo del tiempo del proyecto. Dicho informe se puede consultar en: http://miel.unlam.edu.ar/ – usuario:algebra1 – contraseña: algebra 1

[4] En el Ciclo Básico Común del DIIT se cuenta con la materia Algebra y Geometría Analítica II

[5] Los temas de Complejos y Polinomios no forman parte ahora de la currícula de la materia ya que han sido incorporados al Curso de Admisión

[6] En el Anexo III del informe se presentan algunos de los ejemplos seleccionados para su uso en la materia

[7] El número de docentes se consensuó para poder desarrollar simultáneamente las actividades de los cursos pilotos como así también su supervisión.

[8] Algebra Lineal con aplicaciones, G. Williams; Linear Algebra, W.L.Chen; Álgebra Lineal y sus aplicaciones, G. Strang; Algebra Lineal, J.L. Boldrini.

[9] En el Anexo VI del informe se encuentra la encuesta tomada a los alumnos.

[10] Los resultados generales pueden ser consultados en el informe final.

[11] Un aspecto preocupante es la alta deserción que se produce en los cursos de las materias iniciales. La retención se está encarando desde la actividad en cada materia y con acciones de tutorías y seguimiento.

[12] Se utilizó como base de consulta y ejercitación la plataforma MIEL (Materias Interactivas en Línea) desarrollada por el DIIT.